Por qué los modelos de predicción del tiempo se equivocan (I)
RAMUna de las herramientas más importante que posee el predictor para realizar sus labores de prognosis o predicción son los modelos numéricos de predicción operativa. El “boom” de la Meteorología com...
RAM
Una de las herramientas más importante que posee el predictor para realizar sus labores de prognosis o predicción son los modelos numéricos de predicción operativa. El “boom” de la Meteorología como ciencia práctica se ha debido al advenimiento de la predicción numérica del tiempo por los modelos y a la mejora de estos, al reproducir, parcialmente, el estado de la atmósfera futura. Su disponibilidad en Internet es otra de las razones de su gran popularidad.
La utilidad de esta herramienta es variada. Por un parte, permite conocer mejor los procesos atmosféricos que nos afectan. Hoy en día en muchos centros de predicción se pueden realizar pasadas no operativas con objeto de comprender mejor un determinado temporal de lluvia o viento, el paso de frente, efectos locales, etc. Muchas situaciones atmosféricas pueden ser recreadas a para tal fin. En esa misma línea, es posible disponer de modelos simples educativos para labores pedagógicas. Por otra parte, los modelos numéricos nos permiten disponer de predicciones objetivas desde hoy a varios días, o meses vista, hecho impensable años a tras. Todo ello se ha debido a la mejora de las comunicaciones y el poder de cálculo de los nuevos ordenadores.
Un hecho que ha pasado desapercibido por muchas personas no técnicas es que la llegada de la era de la modelización numérica nos ha llevado a un nuevo campo o tema de interés en Meteorología: la predicibilidad de la atmósfera. Experimentos realizados en los años 60 del siglo pasado pusieron de manifiesto que variando las condiciones iniciales, o de partida, de la pasada de un modelo, las predicciones generadas podían ser muy dispares. Comenzó a hablarse de temas como: la sensibilidad de las predicciones a varios días vista a las condiciones iniciales, predicibilidad de la atmósfera, la atmósfera como sistema caótico, predicibilidad del tiempo, etc. Estos hechos que habían pasado, generalmente, desapercibido hasta esa fecha. Estos temas no lo tocaremos aquí.
Hoy en día sabemos que los modelos numéricos tienen cierto grado o habilidad de predecir el tiempo. En determinadas ocasiones nos encontramos con fallos significativos. Con la sofisticación numérica actual, potentes ordenadores y los medios de observación que disponemos, nos podemos preguntar: por qué se equivocan los modelos en determinadas ocasiones.
Para responder a esta pregunta tendremos que analizar qué es un modelo numérico de predicción del tiempo y qué tiempo o atmósfera predice.
La atmósfera real: ecuaciones dinámicas de evolución
La atmósfera en un sistema dinámico muy complejo, gobernado por unas ecuaciones dinámicas de los fluidos no lineales donde coexisten fenómenos de diferente escala espacial y temporal. El hecho de ser un sistema regido por ecuaciones no lineales en derivadas parciales introduce una dificultad en su resolución: las ecuaciones no tienen soluciones analíticas y exactas. Además, su complejidad se traduce en que algunos fenómenos atmosféricos no son bien conocidos y difícilmente “materializables” con ecuaciones o formulas dinámicas. La atmósfera es un sistema conformado por diferentes procesos que van desde la micro escala a la macro escala, o escala planetaria, pasando por otro sin fin de eslabones. Estos fenómenos interaccionan entre si de forma muy compleja, turbulenta y no lineal.
Todo esto nos lleva a un imperfecto estado del conocimiento del comportamiento de la atmósfera. Pero en el caso que conociéramos todas las ecuaciones y procesos físicos que la rigen, nos encontramos con varios problemas añadidos que vamos a analizar.
Los modelos numéricos: “su atmósfera”
Al no poder resolver las ecuaciones dinámicas en derivadas parciales no lineales que rige la evolución del tiempo, debemos optar por la opción que nos da la modelización numérica, transformado dichas ecuaciones de evolución en ecuaciones discretizadas. Para fijar ideas: representaremos la atmósfera real, continua en el tiempo y en el espacio, como un sistema de puntos dispuestos en una parrilla y distribuidos tridimensionalmente: la atmósfera del modelo no es continua.
Las ecuaciones del modelo pasan a ser ecuaciones que juntas expresan los valores de todas las variables del siguiente paso en función de los valores del paso que está teniendo lugar en el momento actual. Las variables del modelo se predicen en los puntos de rejillas tridimensional a intervalos de tiempo predeterminados y discretos. La atmósfera analizada y predicha ha dejado de ser continua en el tiempo y en el espacio.
Un modelo numérico de predicción, y las técnicas matemáticas asociadas, permite, a partir de unas condiciones iníciales, generar un estado futuro de evolución de la atmósfera de partida. Este proceso de predicción numérica se hace en diferentes fases.
Toma, ingestión y análisis de datos: condiciones iniciales de partida
Para que un modelo numérico “eche a andar” es necesario conocer, al menos, el estado de la atmósfera un instante inicial, o de partida, y lo mejor de las maneras posibles. Aún con los medios que disponemos hoy en día (satélites, radares, estaciones automáticas de superficie, datos de sondeos, etc..), el conocimiento del estado inicial de la atmósfera es limitado en el tiempo y en el espacio. Las observaciones son puntuales, discretas y no cubren a toda la tierra, atmósfera y océanos. Además, muchos datos no son ingestados por el modelo directamente. Mientras que la temperatura observada sí puede ser considerada como una variable directa por el modelo, los datos de radar asociados a ecos de precipitación no son datos que el modelo los pueda tratar directamente.
Muchos datos están provistos de errores que deben ser tratados, eliminados, depurados, etc. Por todos estos motivos, el estado de partida del conocimiento de la atmósfera es incompleto, discreto, etc. y por lo tanto imperfecto.
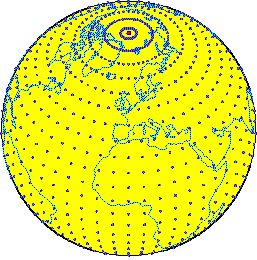
Puntos de rejilla de un modelo global. En dichos puntos se toman las variables de partida o analizadas. Las ecuaciones dinámicas discretizadas trataran obtener las variables en instantes futuros. Los puntos se reparten tridimensionalmente en el espacio esférico.
Este hecho ya introduce una singularidad. Ya que hemos comentados que la evolución de atmósfera es un sistema muy sensible a las condiciones iniciales o de partida: su estado futuro depende significativamente de sus condiciones iniciales.
Si partimos de una atmósfera cuyo estado inicial no es perfectamente conocido, tendremos que tener en mente que la evolución de “esa atmósfera” que analiza el modelo será diferente, y ya de partida, a la real.
Por lo tanto, la calidad y cantidad de los datos de partida en la pasada de un modelo son críticas para la fiabilidad de las predicciones futuras.
Resulta critico tener unas buenas condiciones iniciales de partida para hacer funcionar al modelo. Este hecho es fundamental: es necesario mejorar el incremento y calidad de las observaciones de la atmósfera.
Ajuste de las variables de partida: Inicialización
Un modelo realiza predicciones de ciertas variables atmosféricas o resueltas explícitamente por dicho modelo y, así, construir el futuro estado de la atmósfera. Las variables de partida deben de estar “ajustadas” entre sí. Esas variables provienen de una gran variedad de sensores, altitudes, lugares, etc.. Ese ajuste es necesario ya que las variables a predecir deben estar interrelacionadas por las ecuaciones de la atmósfera que las gobiernan y relacionan dinámicamente. Antes de que el modelo se ponga en marcha, las variables con las que va a trabajar el modelo se tratan, se ajustan y se inicializan para que no generen modos inestables. El proceso de inicialización debe ajustar, sobretodo, los campos de viento y masa con el objeto de no generar estructuras u ondas artificiales, que pueden ser amplificadas posteriormente por el modelo e invalidar su uso, al menos, en las primeras horas.
En muchas ocasiones esta inicialización de las variables de partida elimina información útil que realmente está incluida en las variables de inicio y pueden manifestar algún proceso meteorológico de escala, normalmente, local. La inicialización es un proceso necesario desde el punto de vista numérico.
Antes de iniciar la pasada o predicciones del modelo observamos que la atmósfera de partida “que posee el modelo” no es la atmósfera real: disponemos de información discontinua en el espacio y en el tiempo, las variables a predecir están limitadas por las ecuaciones que controlan a la atmósfera y estas ecuaciones (simplificadas) de la atmósfera limitan y condicionan a los valores de las variables originarias de tal forma que debemos hablar de que un modelo parte con los datos de una atmósfera diferente a la real.
Las ecuaciones que controlan la dinámica de la atmósfera: Predicción
Un modelo numérico trata de resolver y obtener el valor de las variables meteorológicas a predecir, a partir de unas condiciones iniciales dadas. Las ecuaciones que gobiernan el fluido que es la atmósfera está constituidas por ecuaciones diferenciales en derivadas parciales. Estas ecuaciones NO tienen una solución exacta y deben resolver por “métodos numéricos”.
Resolver las ecuaciones originales que controlan la atmósfera no es una tarea inmediata, incluso por métodos numéricos. Lo que se suele hacer es tomar unas aproximaciones o simplificaciones de las ecuaciones originarias y que actúen sobre variables fácilmente observables. Por lo tanto, las ecuaciones (finitas) resueltas por el modelo sólo son una aproximación de las ecuaciones completas de la dinámica atmosférica.
Aunque los métodos numéricos actuales son muy sofisticados, no es menos cierto que sus soluciones son aproximaciones de la realidad.
Por otra parte, los conocimientos que poseemos sobre la dinámica de la atmósfera son importantes pero limitados. Las escalas de fenómenos atmosféricos van desde los muy locales y de corta duración (torbellinos, vientos muy locales, térmicas, etc..) hasta los de escala planetaria (frentes, ondas o perturbaciones de los oestes, etc). Todos ellos son, en menor o mayor grado, importantes y deben ser cuantificados. Esta incertidumbre en el estado de conocimiento y en la física de los fenómenos involucrados es otra fuente de error, mejorable con el tiempo. Pero aún más, si consideramos que un modelo tiene una resolución espacial de 20 ó 30 Km., existirán procesos de dimensiones menores a esa resolución que deberán ser tenidos en cuenta en el propio modelo. Las lluvias generadas por una tormenta de dimensiones del orden de 10 Km. no serán resueltas por el modelo pero sus efectos se deberán incluirse de alguna forma en la modelización.
Las parametrizaciones son procedimientos que tratan de reflejar los procesos que ocurren a una escala inferior a la que el modelo puede reproducir. Todos los procesos que ocurran a una escala menor de la que el modelo maneja deben ser reproducidos mediante parametrizaciones o aproximaciones más simples. Las parametrizaciones más importantes son las relativas a: la convección, radiación, intercambios de calor latente, sensible, etc.. entre al tierra y la atmósfera a nivel del suelo, ...

Existen otras características internas al modelo de las que no vamos hablar (resolución espacial o tamaño de rejilla, orografía del modelo, tipos de suelo del modelo, etc..). Todas ellas están incluidas en el modelo y suponen simplificaciones de la realidad y, por lo tanto, un factor más que nos lleva a alejarnos de lo real.
Todos estos procesos (análisis, inicialización, predicción ...) y otros que no se han mencionado aquí nos hacen llegar a las siguientes conclusiones:
- La atmósfera real versus la atmósfera que ve el modelo. Un modelo numérico parte de los datos de una atmósfera que trata, inicialmente, de parecerse a la real. El modelo arranca y maneja, digamos, “su atmósfera” con unas condiciones de datos iniciales limitados de partida. Cuanto más cerca este ”su atmósfera” de la real, tanto mejor. De cualquier forma, al ser la atmósfera un sistema muy sensible en su evolución a sus condiciones iniciales, tenemos que muchos fallos de predicción de un modelo provienen del imperfecto o inadecuado análisis de los datos partida, del estado actual o inicial.
- Las ecuaciones del modelo son una simplificación de la realidad. Muchos procesos deben ser parametrizados en función de la resolución del modelo. Todo ello hace que, la predicción de la atmósfera del modelo se vaya desviando de la realidad. Antiguamente los modelos se denominaban en función del tipo de atmósfera que trataban de reproducir después de las simplificaciones oportunas, así se trabajaba con modelos barotrópicos, baroclinos, etc..
La atmósfera real y la modelizada
De este somero análisis, podemos intuir algunas de las limitaciones que poseen los modelos a la hora de reproducir los acontecimientos atmosféricos. Un modelo será tanto mejor, en sentido general, cuando sea capaz de disponer y reproducir adecuadamente el estado inicial (tarea nada fácil) y generar unas predicciones de una atmósfera, a partir de las ecuaciones de la dinámica, que no se separé en exceso de la posible evolución real.
Realmente, un modelo si hace predicciones buenas de su atmósfera, con sus ecuaciones matemática, con sus condiciones iniciales, etc. Lo que le exigimos a las salidas del modelo es que sean lo más próxima a la realidad. Pero eso es una argucia humana que trata de conectar y unir la salida de algo abstracto generado por la simulación numérica a la realidad.
Los modelos numéricos tienen cierta habilidad de generar los estados futuros de una atmósfera, su atmósfera, que con los avances técnicos se va acercando más a la realidad, gracias a la propia mejora del modelo, análisis de los datos iniciales observados y la velocidad de proceso de datos. La tarea de predecir el tiempo no es nada fácil, máxime cuando lo que se quiere predecir es un sistema (la atmósfera real) caótico en si mismo: está regido por unas ecuaciones no lineales y muy sensibles a las condiciones iniciales de partida, donde todas las escalas o fenómenos atmosféricos interaccionan entre si de forma no lineal.
Por este, y otros motivos, los modelos numéricos de predicción son herramientas potentísimas, pero ciertamente proclives a equivocarse: desviarse de la realidad atmosférica que es mucho más compleja.
Alguien dijo una vez que las predicciones atmosféricas de los diferentes modelos suelen tener más elementos comunes entre sí que los que existen con la atmósfera real. No sobre estimemos el poder predictor de los modelos numéricos hasta cotas infinitas.
Bajate Hablando en Plata en pdf (166 Kb)