¿A QUÉ DISTANCIA PODEMOS LLEGAR A VER LAS TORMENTAS?
Consideraciones sobre propagación de la luz en medios estratificados en una atmósfera estándar
Francisco José Rodríguez (Mammatus)
[email protected]
Francisco Martín León
[email protected]
Nota de la RAM. Lo que propone nuestro lector, que es a la vez el primer autor del trabajo para que sea tratado en la RAM, no es una simple cuestión anecdótica surgida en una charla de aficionados, sino que involucra una problemática a la que se enfrentan muchos usuarios técnicos influenciados por las condiciones de propagación de ondas electromagnéticas (la luz lo es) en el aire. Por citar solo unos ejemplos, el conocimiento previo de la propagación de la luz en sistemas electro-ópticos es fundamental en campos civiles y militares. Ciertos radares militares deben conocer con antelación las condiciones de propagación de ondas para sus sistemas de radar a bordo de barcos militares. Los submarinos que operan en las zonas fronterizas de la “interfase” aire-mar, deberían conocer en los océanos abiertos la existencia o no de inversiones térmicas y de humedad que pueden condicionar su campo de visión cuando están parcialmente sumergidos.
El estudio de la mejor ubicación de radares meteorológicos y de investigación es otro tema relacionado con el tema que se va a analizar aquí.
Introducción
Muchos de nosotros nos hemos preguntado alguna vez la anterior pregunta cuando contemplamos las cimas o topes de tormentas en la lejanía. A simple vista, la respuesta parece sencilla pero hay que contar con varios factores que tal vez se nos pasan por alto, como mostraremos más adelante.
Los resultados que obtendremos de este artículo no debemos utilizarlos más que para hacernos una idea aproximada de lo que acontece en la realidad, ya que supondremos unas condiciones ideales o estándar de la atmósfera. Las condiciones diarias variarán respecto a las normales y podrán haber diferencias con lo que obtendremos aquí. Esta contribución se divide en dos partes completamente diferenciadas. En la primera parte analizaremos las condiciones de propagación de la luz en un medio ideal no dispersor. En la segunda parte trataremos de explicar los conceptos de rango visual y contraste de objetos iluminados.
El trabajo que presentamos en este número de la RAM se refiere a las condiciones de propagación de la luz en la atmósfera (medio donde varía el índice de refracción). Este a su vez, lo dividimos en varios subapartados y anexos complementarios (para aquellos lectores que quieran profundizar algo más en puntos que no trataremos en el bloque principal). Primero pondremos las bases del problema y sus principios físicos. En la segunda trataremos el caso de una tierra redonda donde el índice de refracción, n, de la atmósfera sea constante. El último caso trataremos la situación en que además n varíe con la altura.
Dejamos para el próximo número de la RAM otros problemas relativos a la dispersión de la luz y contrastes visuales de objetos que tanto influyen en nuestra capacidad de visión.
Entrando en la teoría y su problemática: la curvatura de la tierra y la refracción de la luz en la atmósfera
El problema que proponemos sería evidente y estaría resuelto si estuviéramos situado en una superficie terrestre plana y los haces de luz que emanan del objeto a analizar se propagaran en línea recta y no se dispersan: la realidad es completamente diferente y compleja.
Como todos sabemos, la tierra es redonda y está rodeada de una fina capa de aire, la atmósfera. Por este motivo, cuando se estudia la propagación de la luz (una onda electromagnética, a fin de cuentas) desde un objeto a un observador, nos encontramos que los principales factores que intervienen en la forma de la trayectoria del haz son:
- La curvatura de nuestro planeta, que es la culpable de que no veamos a nuestros vecinos de Grecia por ejemplo, y
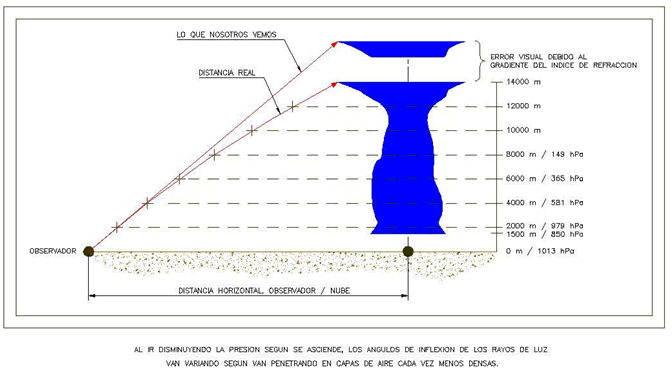
- La curvatura de los rayos de luz al pasar y propagarse por la atmósfera, debido a la variación del índice de refracción, n, en ella. Este factor es fundamental, al considerar la altura real y aparente de los topes nubosos cuando son divisados a grandes distancias: la atmósfera nos “engaña” sobre la altura “real” de las cosas, de tal modo que, a mayor separación y altura del objeto observado, más diferencia habrá entre “lo que vemos” y “lo que realmente es”.
Centrándonos en los topes nubosos como elementos a observar, tenemos que hay otros muchos más factores que entran en juego, como son las condiciones de visibilidad atmosféricas, la agudeza visual de cada individuo, la altura sobre el nivel del mar a la que nos encontramos y los accidentes orográficos u obstáculos entre el observador – tope de la nube. Para la aproximación conceptual que vamos a realizar, desecharemos algunos de estos factores y nos centraremos en los dos que poseen un peso significativo y que hemos comentado con anterioridad. Por lo tanto, partimos de la base de que las condiciones de visibilidad son perfectas y no tenemos obstáculos orográficos de por medio. Pero no solo eso, la luz se propaga sin atenuarse y dispersarse (este problema lo trataremos en el siguiente artículo). La agudeza del individuo es, también, normal. Los objetos a analizar poseen un buen contraste.
Las condiciones meteorológicas existentes en la zona, están íntimamente relacionadas con el factor que hemos comentado antes: la curvatura de los rayos de luz. La trayectoria del haz luminoso va a depender de las condiciones del aire por donde se debe propagar: su temperatura, presión y humedad. Lo explicaremos más adelante.
Cuando miramos a un objeto en la distancia, los haces luminosos atraviesan diferentes capas de aire (según la zona) que están a diferente temperatura y, por lo tanto, a diferente densidad y a diferente presión. Estas variables meteorológicas condicionan el valor y variabilidad del índice de refracción de la capa en cuestión. La atmósfera se puede considerar que está formada por diferentes estratos con propiedades muy parecidas pero no iguales.
Estas capas de aire hacen las veces de un medio refractario, de tal forma que “desvían” levemente los rayos de luz al pasar de una capa a otra. El aire se comporta como un medio donde la refracción de la luz puede ser significativa en ciertas condiciones. De la misma forma que cuando nosotros miramos desde fuera a un objeto que está dentro de una piscina, al salir la luz del agua, la trayectoria del haz se “desvía”, haciéndonos ver que el objeto está más cerca de lo que en realidad está. Con el aire ocurre algo parecido, pero lógicamente a menor escala, al existir menor diferencia de densidades entre una capa y otra.
Todo estos hechos vienen definidos por la ley de Snell (no vamos a entrar en detalle en describir esta ley fundamental de la Física):
“El ángulo que forma el rayo refractado con la normal (ángulo de refracción) está relacionado con elángulo de incidencia: n1senai = n2 sen ar”
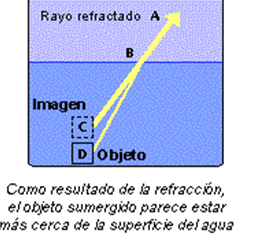
O dicho de otra forma, y para el caso de la luz, cuando un rayo luminoso pasa de un medio a otro de menor índice de refracción, el haz emergente se desvía de la normal a la superficie que separa a ambos medios. En este esquema, podemos verlo más claramente:
Un observador, “A”, situado sobre la superficie y en el aire, verá el objeto sumergido, “D”, más cerca ya que los rayos que emanan de él cambian de dirección al pasar del agua al aire. Ambos medios poseen índice de refracción diferentes, mayor del agua que el del aire. En la atmósfera ocurre algo parecido, el índice de refracción decrece con la altura. Un tope nubosos situado muy alto y en la lejanía debe llegar a los ojos del observador, atravesando diferentes capas con valores de n. El resultado es que, en condiciones normales, los haces se curvan hacia abajo y el observador verá que el objeto se encuentra situado más alto que la realidad.
Como vimos antes, y en una primera aproximación, la atmósfera podemos considerarla como un conjunto de capas con índices de refracción muy próximos a la unidad, pero diferentes. De esta forma, el índice de refracción de la atmósfera terrestre disminuye monótonamente con la altura, desde su valor superficial (cercano a 1,00029) hasta el valor en el espacio (próximo a 1,0000) en la cima de la atmósfera (solo en el vacío n es igual a 1).
Un rayo de luz proveniente del Sol pasa, en condiciones normales, por sucesivas capas atmosféricas donde el índice de refracción decrece con la altura. Se supone la superficie de la Tierra plana.
En la figura adjunta, el Sol, S, que vemos estaría aparentemente más alto que el real.
De este modo, y al ir disminuyendo la presión, temperatura y densidad del aire a medida que subimos, también va variando el valor del índice de refracción. Los valores que toma el índice de refracción, n, con la altura para una atmósfera estándar son:
| Índice, n | Altura (km) |
|---|---|
| 1,000000 | 14 |
| 1,00003625 | 12 |
| 1,0000725 | 10 |
| 1,00010875 | 8 |
| 1,00018125 | 6 |
| 1,0002175 | 4 |
| 1,00025375 | 2 |
| 1,00029 | 0 |
| Tabla I. Valores del índice n de refracción con la altura en una atmósfera estándar | |
En el Anexo I puedes encontrar una breve descripción de cómo varía n con las variables atmosféricas, P y T. No entraremos en detalle aquí sobre este tema.
También existe otro factor, que es el de distancia horizontal observador –tope de la nube. Según nos acercamos a la nube atravesamos capas de aire donde las variaciones de densidad y temperatura serán menores que cuando nos enfrentamos al problema de una nube muy lejana.
Aplicando la ley de la refracción, obtenemos que la variación en la altura “real” con lo que vemos es aproximadamente un 1% cada 1000 metros de ascensión en los primeros 200 km.
Por lo tanto, la elevación aparente del tope nubosos, es notoria cuando nos encontramos a grandes distancias y o cuando las condiciones atmosféricas sean tales que el haz se curve demasiado. El problema se complica al considerar la tierra como superficie no plana y la variación de n con la altura.
Haremos un análisis, a este problema complejo, mediante aproximaciones. En primer lugar supondremos que n es constante y la tierra es redonda, posteriormente consideraremos las variaciones del índice de refracción con la altura y su influencia en el problema que nos concierne.
Refracción en la baja troposfera en una tierra redonda: acercándonos a la realidad
Primero vamos a analizar unos datos de partida y de referencia que deberemos tener en cuenta.
Supondremos una tierra redonda con un radio de 6378 Km. La altura de la nube que vamos a someter al cálculo es de 14 Km. Lo primero que se nos viene a la mente es cómo determinar la altura de una nube que estamos viendo. No vamos a describir algunos de los procesos que nos pueden ser útiles para determinar la altura de una nube. Os remitimos al Anexo II para daros unas ideas orientativas de cómo obtener la altura nubosa. La triangulación por teodolitos es un método terrestre muy empleado.
Obviamente, desechamos la altura del individuo, ya que en comparación con el radio de la tierra, es un dato insignificante. Supondremos que se encuentra al nivel del mar, sin obstáculos próximos y una atmósfera ideal con muy buena visibilidad.
El procedimiento que seguiremos es de aproximaciones sucesivas, desde caso más simple al caso más complejo.
a. El índice de refracción, n, es constante
En este caso los rayos que le lleguen al observador no se curvarán y la visual que une el tope de la nube – observador será una línea recta en una tierra redonda.
Vamos a empezar viendo a qué distancia máxima podemos llegar a ver el techo de la nube, o sea, el límite a partir del cual nos será imposible divisar dicha nube haya las condiciones que haya.
Aquí tenemos un esquema en el que se ve una “porción” de la tierra:
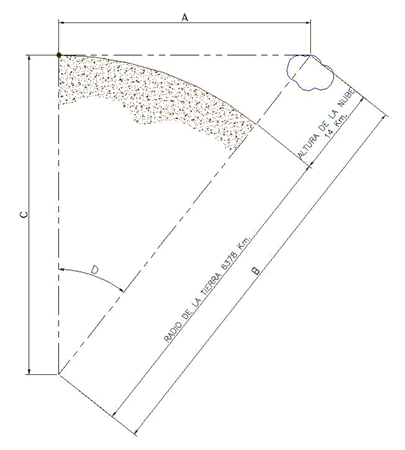
En este esquema tenemos varios datos:
A: Distancia máxima a la que podremos llegar a ver la nube, a determinar, d
B: Radio de la tierra mas altura de la nube: R+h
C: Radio de la tierra, R
D: Angulo que forman las distancias.
Ya que nuestra mirada al horizonte siempre es horizontal, formamos para nuestro cálculo un triangulo rectángulo.
Trigonométricamente hablando:
cos D = C/B= R / R+h
En nuestro ejemplo
cos D = 6378 / (6378+14)
Angulo D = 3.7928°
Por otra parte,
sen D= d/ R +h
Como sen 2 D + cos 2 D = 1, (d /R+h) 2 + (R /R+h) 2 = 1
Despejando d, tenemos:
d 2 = h 2 + (2hR) como el primer término es muy pequeño comparado con el primero, resulta que
(1)
d 2 = 2hREsta expresión relaciona la distancia, d , a la que podemos ver la cima de un objeto de altura h para una tierra uniforme y con un índice de refracción constante (el rayo se propaga en línea recta, en este caso dn/dh=0).
O en nuestro caso:
A = (sen D) x B
A = sen 3.7928° x 6392
Distancia A = 422.8 km
Esto es que la distancia máxima (teórica) a la que se puede ver una cima de una nube de 14 Km. de altura son 422.8 Km, en las condiciones ideales comentadas.
Partiendo de este dato se ha hecho una pequeña tabla en la que aparecen las distancias máximas a las que se pueden ver los techos de las nubes.
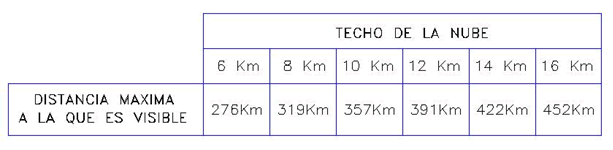
Un hecho importante es que hemos considerado la tierra con un radio R, y por lo tanto su curvatura es 1/R, y el haz luminoso se describe una línea recta, ya que n es constante. Si hacemos una abstracción muy útil podemos considerar la tierra plana y haz curvándose hacia arriba con la misma curvatura que la tierra. Dicho de otro modo; podemos considerar que todo ocurre como si la tierra fuera plana y el haz se curva hacia arriba. Solo hacemos un cambio de referencias: Un hipotético observador que se desplazara por el haz podría afirmar, en su movimiento relativo, que la tierra es plana y la trayectoria que sigue él es tal que se curva hacia arriba hasta llegar al tope de la nube. Hemos transferido la curvatura de la tierra a la curvatura del haz, desde el punto de vista relativo.
Con todo esto, nos podemos hacer una idea de lo que podemos llegar a ver. Vamos a poner otro ejemplo ilustrativo.
Imagínense que están en la Ciudad (A), y hay una tormenta en la Ciudad (B). Estas dos ciudades están separadas en línea recta por 350 Km. Así mismo vemos que los topes de la nube tormentosa están a 14 Km. Hace en la ciudad (A) un día magnífico y la visibilidad es estupenda. Si tenemos buena vista, y dirigimos nuestra mirada a la ciudad (B) llegamos a ver la parte mas alta de la nube, pero ¿Cuánto vemos de ella?
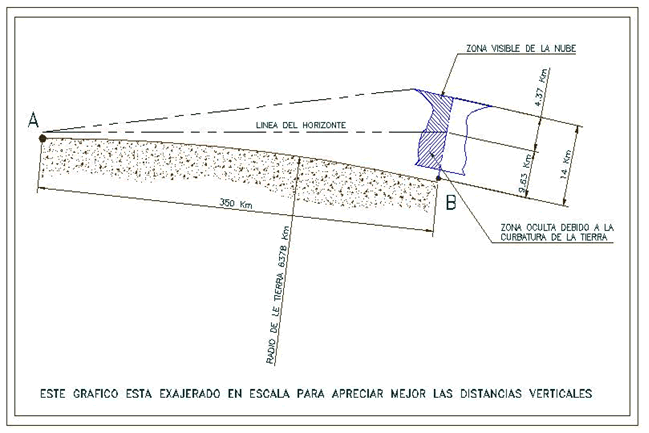
Por medio de las operaciones trigonométricas antes explicadas, sacamos el resultado, y en este caso concreto, la distancia de 4.37 Km. es lo que veríamos de nube, equivaldría a algo menos de 1°.
Aclaraciones: Muchos pensarán que las distancias entre A y B no son del todo correctas, puesto que para que fuera una distancia exacta, habría que medir la longitud de la cuerda que forman A y B con el Radio de la tierra. Es cierto, pero no lo he hecho así porque la diferencia es ínfima. De hecho si la distancia en línea recta es de 350 Km., la cuerda formada por esa distancia y el radio de la tierra sería de 350.043 Km. O sea 43 metros sobre 350 Km. Un 0.012%.
Ahora vamos a ver un ejemplo real de todo esto:

Esta imagen está tomada desde la localidad de Coslada (Madrid) apuntando hacia el Sureste. Es el día 2 de Agosto del 2002 en el que una curiosa línea de Cb poco activos y con sus bases muy altas se paseó por delante de nosotros en dirección Oeste – Este.
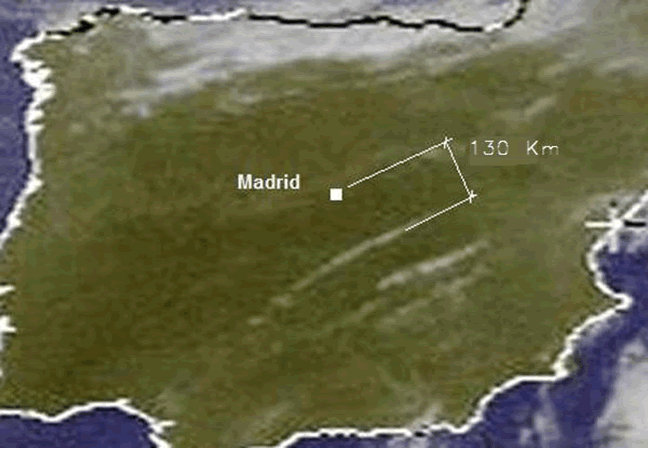
Aquí vemos la imagen satélite de ese día en el que se observa a la perfección la curiosa formación nubosa en forma de aguja. Como he marcado, la distancia en línea recta desde Madrid a dicha formación es de 130 Km.
Recapitulando datos, tenemos:
Distancia en línea recta a la nube: 130 Km.
Techo de la nube: 10 Km.
Radio de la tierra: 6378 Km.
Situación: 650 m. snm (metros sobre el nivel del mar)
Orografía: Plana
Visibilidad: Muy buena
Haciendo los cálculos hechos anteriormente, nos da el siguiente resultado:
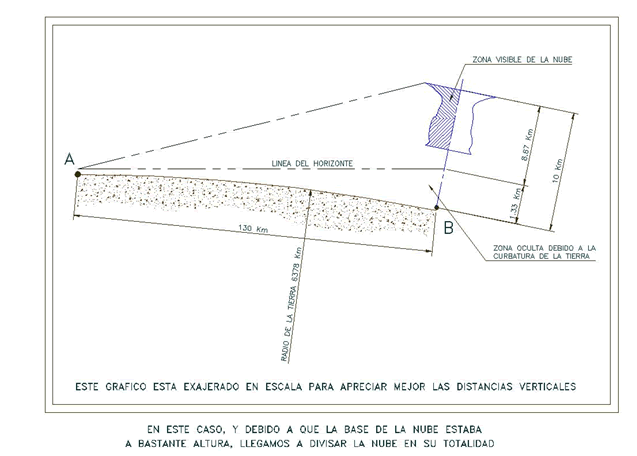

Resumiendo, con esto podemos saber que por ejemplo no es nada descabellado poder ver tormentas en Albacete ó Valencia desde Madrid (de echo yo (Francisco José) desde mi casa y mirando al Sureste, he visto yunques de Cb que en esos momentos descargaban en Albacete).
O como algún amigo nos comentó hace tiempo, que vio las tormentas de Barcelona desde Valencia. Y si apuramos más, ya que las distancias se miden en líneas rectas y no en Km. de carreteras, si trazásemos un radio de 400 Km. alrededor de Madrid, abarcaríamos muchas zonas, mas de las que nos pensamos. Creemos que solo quedaría fuera de nuestro campo de visión, la parte mas al NO de Galicia (descartando el Sistema Central por supuesto), el extremo NE de Catalunya, y el S de Andalucía.
Todo esto desde el punto de vista teórico. Demos un paso más.
En los anteriores ejemplos hemos supuesto que el índice de refracción, n, no variaba con la altura. Vimos que mediante una transformación conceptual, y para una tierra de radio R o curvatura 1/R, era posible obtener una relación simple y un modelo conceptual asociado a tierra plana: el haz recto lo transformábamos a haz curvo sin más que “pasarle” la curvatura de la tierra, siendo esta plana. Ahora vamos a suponer que el índice n varía con la altura.
Para ello partimos de una ecuación de propagación de ondas en la troposfera que relaciona la variación del ángulo del rayo la distancia (su demostración cae fuera de los límites de este trabajo). Como siempre, lo que queremos determinar es la distancia d que alcanza un rayo de luz que provienen de un objeto o topes nubosos a altura h. El observador se encuentra a una altura ho. R es el radio de la tierra (>>> h y ho) y se supone que n varia poco con la altura (rayo casi paralelo a la superficie de la tierra, pero no igual). Estamos siempre dentro de la troposfera o la tropopausa.
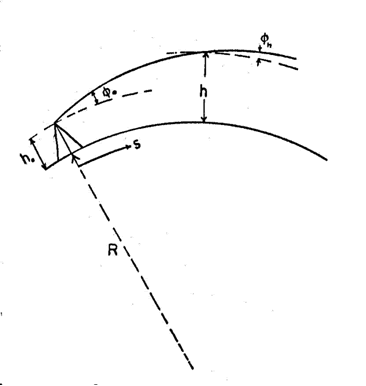
Trayectoria esquemática de un haz troposférico para una tierra de radio R.
El índice de refracción n varía con la altura
La ecuación que relaciona la altura h con la distancia s viene dada por:
(2)
d 2h / ds 2 = 1/R + dn/dh
Que es una ecuación diferencial fácil de resolver. Observamos que si el índice n es constante con la altura (dn/dh=0) la ecuación (2) admite como solución la (1), salvo constantes, o sea, estaríamos en el caso a.
Por otra parte, el ángulo Φ que forma el haz con la superficie de la tierra es pequeño al suponer que n varia poco con la altura, en este caso
(3)
Φ = Φ h/Φ s
Uniendo la (2) y (3), y poniendo (3) en forma diferencial, llegamos a que,
(4)
d Φ /ds = 1/R + dn/dh
Esta expresión nos dice cómo varia el ángulo de refracción Φ en la troposfera para una tierra con la curvatura 1/R y en la que el índice n varia con la altura. Un caso especial es cuando la variación de n con h (que es negativa) coincide con la curvatura de la tierra (1/R). En este caso Φ es constante y el rayo se propaga paralelo a la tierra.
Llama la atención que dn/dh tenga las dimensiones de curvatura (m -1). Es muy común hacer otro cambio de referencia e imaginar a una tierra ficticia cuyo radio de curvatura sea el término de la derecha de la ecuación 4 de forma que la “nueva tierra” tenga un radio R’ tal que:
(5)
1/R’ = 1/R +dn/dh
Esta tierra ficticia es mayor que la real,al ser dn/dh negativo (R'>R), nos permitirá reducir el problema anterior a uno más simple. De nuevo, la tierra ficticia de trabajo "absorbe" la variación de n con h y la ecuación 4 podemos rescribirla como:
(6)
d Φ /ds= 1/R' o d 2H / ds 2 = 1/R'
Si despejamos R’ de (5) tenemos que el radio de la tierra ficticia es tal que:
R’= R/ ( 1 + R dn/dh)
Si tomamos un valor de dn/dh = -4 10 –8 m -1 que aproximadamente es -1 / (4 R), resulta un valor de R’=4/3 R. A esta aproximación y modelo asociado se le denomina modelo de los 4/3. Esta aproximación mediante el modelo de 4/3 es muy utilizada en meteorología radárica terrestre a la hora de calcular la elevación del haz medio del radar cuando el pulso electromagnético se aleja de él con la distancia.
Pero esta última expresión equivale al caso “a”: Una tierra ficticia de radio de curvatura 1/R’ donde ficticiamente n no varía con la altura, cuenta ya con una solución que es inmediata: la ecuación (1) pero cambiando R por R’.
d 2 = 2hR’
Normalmente dn/dh no es conocido y a efectos prácticos se suele tomar un valor normal o estándar, que ya ha sido comentado con anterioridad.
Por lo tanto y como estamos en el caso “a”, podemos describir la trayectoria del haz suponiendo que la tierra ficticia es plana y que la curvatura la “absorbe” el rayo de luz que se curva también hacia arriba.
Las ecuaciones que relacionan h y d, usando el modelo de los 4/3 y cuando nuestra visual forma un ángulo Φ respecto a la superficie terrestre y al estar situado a una altura ho, son:
s = R' arcsen ( d cosΦ / (R'+h))
h = (R'+ho) ( cosΦ / cos(Φ + (s/R')) - R'
con:
R’ = 4/3 R
s representa la distancia entre la base de la nube sobre la superficie de terrestre al observador. Ver figura superior para relacionar las variables que estamos comentando.
Fijando ideas y conclusiones de estos apartados
Después de estas explicaciones vamos a daros un diagrama útil y aproximado de la relación de distancias y alturas visuales que trate de resumir lo que hemos comentado hasta aquí. Como siempre, estamos trabajando en una atmósfera estándar donde el índice de refracción varíe con la altura y en una tierra redonda. El haz luminoso no se dispersa con la distancia, el día es claro y limpio, y no hay obstáculos. Supongamos un observador al nivel del mar.
Tomaremos la siguiente figura como referencia. Las curvas fueron calculadas para días de verano en Suecia en que las alturas de las nubes fueron calculadas por triangulación y con teodolitos. Las distancias también fueron obtenidas por métodos precisos.
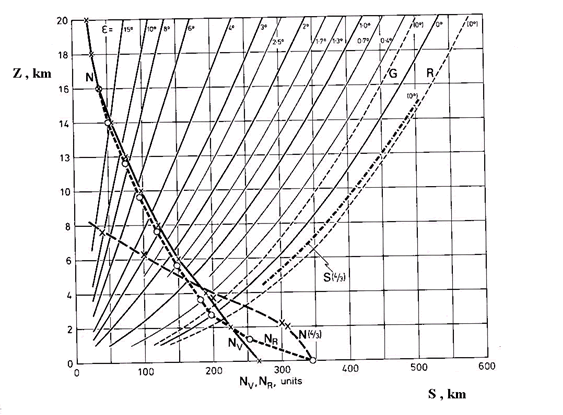
En esta figura presentamos la elevación del haz teórico para distintos ángulos de visión con la distancia. La tierra la suponemos redonda, pero en el diagrama aparece el eje S como plano ( la curvatura del haz ha “absorbido” la variación de n con la altura). El observador mira con diferentes elevaciones visuales, Φ. Su visual la asimilamos a un rayo ideal que llega desde el objeto. S se supone que es la distancia a la que se encuentra el objeto.
Mediante el diagrama anterior podemos ver que si la nube se encuentra a (S=) 200 km de distancia y la miramos con un ángulo visual de (ε=) 0deg; tenemos que, teóricamente, se verían solo los topes de nubes de hasta 2 km o más de altura. Nubes de poco desarrollo que no lleguen a alcanzar los 2 km de altura quedan por debajo de nuestra visual debido al curvamiento del haz hacia arriba.
En esas condiciones, la visual estará a 6 km de altura a unos 300 km de distancia y las nubes que superen este nivel si serán observadas.
Suponiendo que una nube tormentosa llegue a 14 km de altura, tendremos que podrá situarse, teóricamente, a 450 km como máximo de distancia para ser vista. Topes convectivos de 18 km de altura serían vistos desde 500 km de distancia, según el diagrama anterior y en condiciones comentadas con anterioridad.
En Ludlam (1980) se sugiere una formula muy simple que relaciona la trayectoria del haz y altura alcanzada, Z, con la distancia S, para elevaciones visuales y longitudes de ondas de la luz,ε, en rangos inferiores a 200 km.
Z = s tangε + s2 / 2 f R
Donde:
R: es el radio de la tierra.
ε: es el ángulo de visión
f: es un factor (=1.15)
Obsérvese que z=f(s,ε), y para un ángulo dado, s toma la forma de una parábola invertida que pasa por el origen.
Hay un pero ....
Una vez más, todo esto es en teoría. Hasta ahora no hemos considerado un problema adicional y es que los rayos de luz que nos llegan desde objetos lejanos y durante el día se van dispersando y llega un momento que nuestra visual óptica y rango de visión se limita a distancias menores de las comentadas aquí. No podemos percibir objetos que se encuentren a 500 km de distancia ya que el rango de visión del ser humano es limitado ¿Pero hasta cuánto y por qué?. Lo veremos en el próximo número de la RAM.
Agradecimientos:
A Pablo Ruiz (Cumulonimbus) y a otras personas del foro de Meteored que nos enviaron sugerencias.
Anexo I
El índice de refracción, n, y su relación con las variables atmosféricas
El índice de refracción en la atmósfera, n, para las frecuencias de radio entre HF y UHF viene dado por:
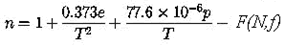
donde:
e - presión parcial del vapor de agua (hPa)
T - temperatura absoluta (K)
p - presión atmosférica (hPa)
F - función que depende de:
Ne - densidad de electrones libres (m-3)
f - radio frecuencia (MHz)
Puesto que n toma valores muy próximos a 1.0, y sus variaciones son muy pequeñas, es muy útil trabajar con el índice de refractividad, N, dado por:
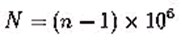
Analicemos las contribuciones atmosféricas de las variables sobre N o n.
El primer término de la ecuación, representa la contribución de la humedad. Las moléculas del agua tienen un momento dipolar que varía con la frecuencia de la radiación electromagnética. En las frecuencias de la luz visible solamente el campo eléctrico polarizado de las moléculas del vapor de agua contribuye.
El segundo término representa la contribución de la densidad. El tercer término suele ser significativo en altitudes muy elevadas (más allá de los 50 km de altura) donde la densidad de los electrones es muy elevada. Este término se puede despreciar en la troposfera.
La figura adjunta muestra conceptualmente la contribución relativa de los términos de humedad y densidad a la refractividad para una atmósfera estándar en EEUU, por debajo de los 20 km (los perfiles de humedad y temperatura se muestran en el centro y lado izquierdo).
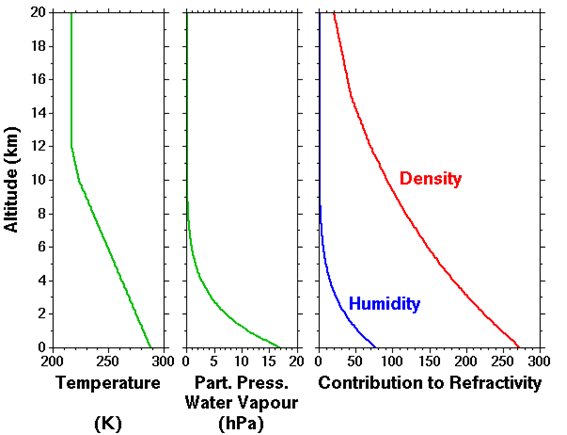
Observamos que las máximas contribuciones de N provienen de la densidad y de la humedad. En el caso de la densidad, es la distribución de la temperatura la que más peso tiene en los valores de N. Estas contribuciones se maximizan en niveles bajos. A pesar de que la humedad contribuya en menor medida que la densidad del aire (que está fuertemente influenciada por la temperatura, T, en todos los niveles), en determinadas ocasiones el índice N, y por lo tanto n, pueden estar significativamente influenciado por inversiones de humedad o por capas que posean variaciones fuertes de contenido de humedad. Más acusado es el caso en que existan fuertes gradientes de temperatura, inversiones térmicas, etc.. en estas condiciones pueden aparecer efectos ópticos muy acusados (espejismos superiores e inferiores).
Por lo tanto, los valores de N pueden tomarse de está ecuación (donde se han despreciados varios términos poco significativos), y que se suelen utilizar en la práctica habitual:
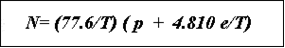
Así, cerca del nivel del mar n puede tomar valores de n=1,0003 y N= 300. En condiciones normales los índices n y N decrecen con la altura y en la cima de la atmósfera, donde reina el vacío, n=1 y N=0. Por lo tanto, dn/dh<0, siendo h la altura. La variación del índice de refracción con la altura, dn/dh, es casi constante y, para muchos casos, se suele tomar un valor de - 4 x 10 -8 m-1. Una vez más, esta variación con la altura puede verse modificada por la presencia de inversiones térmicas y/o de humedad.
Al decrecer n o N con la altura, el haz luminoso se curva hacia abajo pero de forma menos rápida que la curvatura de la tierra y, por eso, el horizonte visible está más lejos que el horizonte geométrico. Cuando el sol está por debajo del horizonte geométrico, su luz todavía nos llega y aparece, por tanto, visible y elevado sobre el horizonte geométrico.
Hay que mencionar que las formulas (1) y (2) son las más usadas. Otras aproximaciones más “finas” incluyen una función de la longitud de onda de la radiación considerada.
Anexo II
Cómo determinar la altura aproximada de una nube
Existen métodos muy precisos que requieren el uso de teodolitos y triangulaciones pero no serán tratados aquí. Vamos a indicaros como podemos obtener la altura de una nube, de forma aproximada.
I.- Imagen IR y mapas de altura o sondeos termodinámicos
Para ello, partimos que disponemos de una imagen IR de satélite, sondeo cercano o mapas de topografías relativas.
La imagen IR de los satélites nos informa de la temperatura de brillo de la superficie emisora: el tope o cima de la masa nubosa, por ejemplo. Para el caso de nubes altas y tormentosas muy profundas que lleguen a niveles altos de la troposfera, la temperatura de brillo, o de emisión, que observamos en la imagen IR es casi igual a al temperatura del tope de la nube. Cuando consideramos nubes más bajas, su temperatura de brillo (IR) y la temperatura real pueden diferir por los problemas de absorción atmosférica. Al considerar nubes de desarrollo vertical haremos la suposición que la temperatura de brillo y la real coinciden. Algunas imágenes que aparecen en Internet del canal IR están realzadas según la temperatura de los topes nubosos. De una simple inspección visual podríamos obtener la temperatura de la cima de dicha nube, supongamos que medimos unos – 50º --55º C. Si tomos un sondeo próximo en el tiempo y en el espacio, que nos da el perfil de temperatura, y presión frente a la altura, tendríamos resuelto el problema ya que podríamos obtener la altura y el nivel de presión del tope nuboso sin más que saber su temperatura.
Si no disponemos de un sondeo real próximo podemos utilizar el asociado a una atmósfera standard donde el perfil vertical P/h – T es conocido, siendo P la presión, h la altura y T la temperatura.
Si no disponemos de dichos sondeos deberíamos utilizar las salidas de modelos numéricos de alta resolución vertical. La altura a la que se alcanza una temperatura dada y en un punto determinado se calcula buscando en la vertical de dicho punto el nivel del modelo a la que se alcanzaría dicha temperatura directamente o por interpolación.
EUMETSAT genera productos de altura de nubes a gran escala (CTH, cloud top height), con baja resolución. Puedes ver un ejemplo de ello en:
O el último producto generado del tipo CTH en:
A veces, es suficiente trabajar con los valores estadísticos medios de las alturas que pueden alcanzar, por ejemplo, los Cb en nuestras latitudes o la misma altura de la tropopausa, como base de referencia. Esta aproximación grosera puede ser suficientemente buena.
II.- Productos radar de altura de ecos de precipitación: echotops
Algunas instituciones meteorológicas suministran un producto de la altura que alcanzan los ecos de precipitación detectados por los radares meteorológicos. Esta información podría ser muy útil para nuestros propósitos.
Los radares meteorológicos modernos exploran volumétricamente la zona circundante en distancias de centenas de kms. En esas exploraciones, realizadas a diferentes elevaciones, se pueden llegar a detectar las alturas máximas a las que existen ecos de precipitación (que no nubes). Dependiendo de su táctica de exploración, sensibilidad del radar y umbral fijado como señal de los topes de los ecos de precipitación, etc.. tendremos que, mediante un tratamiento adecuado de los datos, la posibilidad de analizar a qué altura existen tales ecos y, por tanto, tener un idea de la altura de la nube. Siempre la altura de la nube será mayor que la altura del echotop.
Desgraciadamente en España no están disponibles dichos productos radar en Internet y en nuestra zona de interés. El echotop (producto de alturas de ecos de precipitación) solo tiene sentido allí donde existan nubes que contengan precipitación en su seno. Las nubes convectivas maduras sí poseen precipitación embebida y llegan a dar alturas de ecos elevados.
Bibliografía
Clouds and Storms, 1980 . Ludlam, F. H, The Pensylvania State University Press 400 pp.
Agradecimientos. A los comentarios positivos y enreiquecedores de "Cumulonimbus" y de otros "foreros" de meteorología.