Atenuación de la señal del radar meteorológico por precipitación
Entre los fenómenos que afectan la medida de la precipitación a partir de datos radar está el de la atenuación del haz por el medio atmosférico, que en el caso de los radares de banda C como los del INM tiene una gran importancia cuando hay lluvia presente.
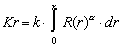
Autor: Ramón Pascual (*) [email protected]
y
Marc Berenguer(**)[email protected]
Artículo de enero de 2003. Recuperado en agosto de 2013
(*) Centre Meteorològic Territorial a Catalunya. Instituto Nacional de Meteorología. Barcelona
(**) Grup de Recerca Aplicada en HIdrometeorologia (GRAHI). Universitat Politècnica de Catalunya. Barcelona
CONCEPTOS BÁSICOS
Entre los fenómenos que afectan la medida de la precipitación a partir de datos radar está el de la atenuación del haz por el medio atmosférico, que en el caso de los radares de banda C como los del INM tiene una gran importancia cuando hay lluvia presente. Este efecto no solo afecta a la medida de la precipitación en términos de milímetros acumulados o a la intensidad instantánea, como también lo hace la relación Z-R adoptada, por ejemplo, sino que también determina en gran medida la interpretación subjetiva o el análisis objetivo del campo de reflectividad radar instantánea (diezminutal en el caso del INM) pudiendo dar lugar a subestimaciones de la intensidad de una lluvia o chubasco e incluso al desconocimiento de la presencia de precipitación en un área concreta.
Definición de atenuación: Es la pérdida de potencia del haz de radiación electromagnética emitido por el radar al atravesar el medio en el que viaja. La atenuación afecta al camino de ida y vuelta del haz del radar.
En esta breve nota no se hace referencia al fenómeno de pérdida de potencia del haz del radar al atravesar el radomo mojado por precipitación actual o reciente sobre el radar ni se debe confundir la atenuación con el apantallamiento total o parcial del haz debido a obstáculos orográficos fijos. En el caso del radomo mojado la pérdida de señal en la imagen radar es generalizada y no restringida a una área concreta como en el caso de la atenuación.
La atenuación del haz se debe a tres componentes atmosféricos principalmente:
- Por gases (Oxígeno molecular y vapor de agua).
- Por nubes y nieblas.
- Por precipitaciones: lluvia, nieve y granizo.
Los fenómenos físicos implicados en el proceso de la atenuación son dos:
- Absorción de parte de la energía incidente.
- Dispersión (scattering) de esta energía.
En general la atenuación viene definida por la expresión:
dP = -kPdr
Ec. 1
donde dP/dr es la variación de la potencia con la distancia y k es el Coeficiente de atenuación y se suele expresar en dB/km. Por lo tanto cuanto más largo sea el camino recorrido por el haz mayor será en general la atenuación.
La atenuación depende en todos los casos de la longitud de onda de la señal que se está propagando en el espacio y en general cuanto mayor sea ésta (y por lo tanto menor su frecuencia) menor será también la atenuación. La atenuación por gases atmosféricos (absorción) se puede considerar prácticamente nula para longitudes de onda superiores a varios centímetros. La atenuación por nubes y lluvia debe ser considerada para longitudes inferiores a los 10 cm (banda S), y es especialmente pronunciada por debajo de los 3 cm (banda X). El efecto del polvo, la calima y el humo es también prácticamente despreciable.
Se puede expresar el efecto combinado de la absorción y la dispersión mediante la fórmula:
Q<sub>t</sub> = Q<sub>s</sub> + Q<sub>a</sub>
Ec. 2
donde Qt es la atenuación total, Qs la sección efectiva de dispersión y Qa la sección efectiva de absorción de la partícula.
Atenuación por nubes
Es muy variable ya que depende de la cantidad de nubes y de los tipos presentes, tanto en lo que hace referencia a su espesor como a su composición, aunque las nubes compuestas casi exclusivamente por partículas de hielo tienen un efecto prácticamente despreciable. Este tipo de atenuación es muy significativo en los radares de banda X y mucho menor en los de banda C (como el del INM y la mayoría de los radares meteorológicos operativos) y S especialmente (Tabla 1). Depende de la longitud de onda del haz emitido, de la temperatura de la nube, del contenido de agua líquida y de la fase de la precipitación.
| Visibilidad (m) | Atenuación (dB/km) | |
| l = 3.2 cm (Banda X) | l = 10 cm (Banda S) | |
| 90 | 0.04 | 0.004 |
| 300 | 0.007 | 0.001 |
| Tabla 1: Atenuación del haz radar en una niebla para radares de banda X y S. Los valores para radares de banda C se encuentran entre los presentados para las otras dos longitudes de onda | ||
Atenuación por lluvia
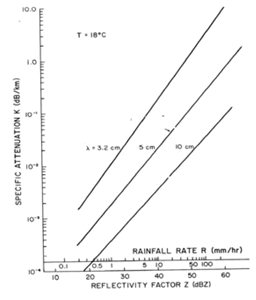
Depende de la intensidad de la precipitación (medida en mm/h), de manera que cuanto más intensa es ésta mayor es la atenuación (Fig. 1 y Tabla 2) . Los radares de banda C sufren una atenuación media-alta de este tipo y por encima de los 10 cm de longitud de onda los efectos decrecen rápidamente.
Se puede expresar la atenuación como:
Ec. 3
donde los coeficientes k y ? dependen principalmente de la frecuencia del radar así como de la temperatura y tipo de lluvia. Por lo tanto la atenuación depende de la longitud del camino del haz que atraviesa una zona con precipitación pero también de la intensidad de ésta. Tanto un camino largo con precipitación de intensidad moderada como un camino más corto con precipitación fuerte pueden determinar una atenuación importante.
Intensidad de la precipitación (mm/h) | Atenuación (dB/km) | |
l= 3.2 cm | l = 10 cm | |
12.5 | 0.238 | 0.00364 |
50 | 1.26 | 0.0149 |
100 | 2.8 | 0.0311 |
| Tabla 2: Atenuación por lluvia para radares de banda X y S. Los valores para radares de banda C se encuentran entre los presentados para las otras dos longitudes de onda. | ||
Para un longitud de onda de 3.2 cm una precipitación de 50 mm/h atenúa 5,3 veces más que una 4 veces inferior. Para 50 mm/h una longitud de onda de 3.2 cm se atenúa casi 85 veces más que una de 10 cm. Se observa de esta manera la enorme importancia de la longitud de onda y de la intensidad de la precipitación en el proceso de la atenuación por lluvia de la energía radiada por el radar.
Atenuación por nieve
Para longitudes de onda superiores a los 10 cm la atenuación por nieve seca puede considerarse despreciable pero para longitudes de onda menores puede ser apreciable, especialmente si el rango y la intensidad de la precipitación son grandes. Para nieve húmeda, la que se encuentra hasta unos 500 m por encima del nivel de fusión, la atenuación será mucho mayor. Por esta razón la atenuación al atravesar el haz la banda brillante es también muy importante (Es el efecto inverso precisamente a la aparición de esta banda de máxima reflectividad).
Atenuación por granizo
Es muy difícil cuantificarla ya que la precipitación en forma de granizo o pedrisco es muy variable en duración, extensión e intensidad (cantidad de granos y distribución de tamaños).
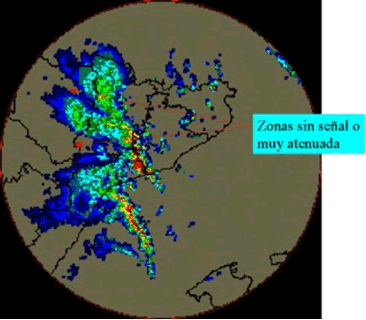
Identificación del efecto de la atenuación
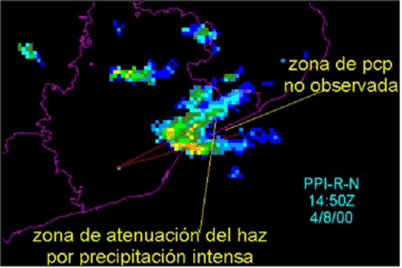
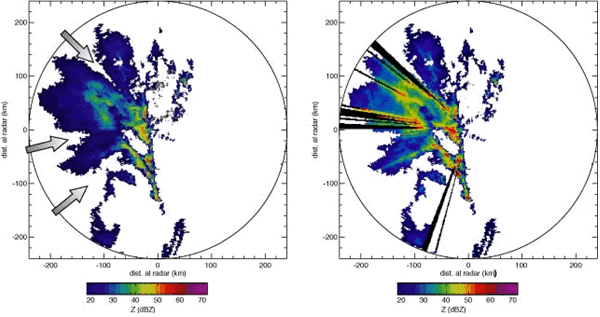
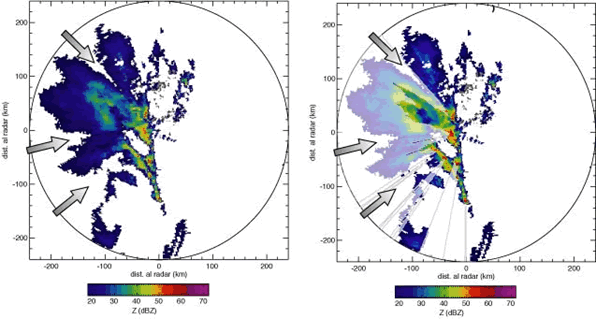
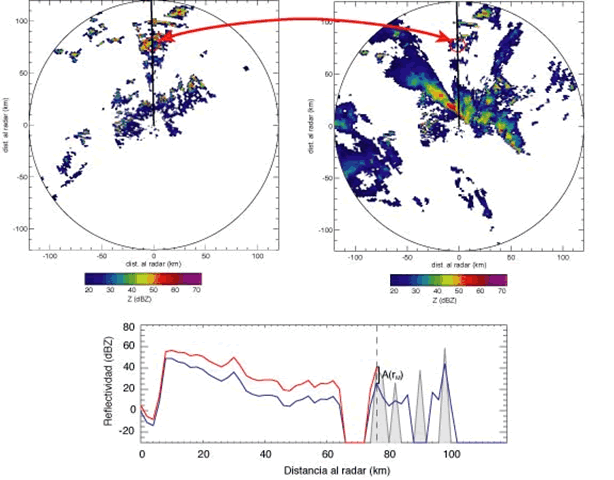
La atenuación debida a la precipitación se puede reconocer a partir de la observación de “sombras” en la imagen radar aparecidas detrás (desde el punto de vista del radar) de áreas de precipitación intensa (Fig. 2 y Fig. 3). La pérdida de señal se produce tanto en el camino de ida como en el camino de vuelta del haz. La corrección de la atenuación es un proceso muy importante (y muy complejo) en la estimación cuantitativa de la precipitación a partir del dato radar.
CORRECCIÓN DE LA ATENUACIÓN DE LA SEÑAL DEL RADAR
En la actualidad prácticamente no existen metodologías operacionales para la corrección de la atenuación en radares terrestres. Se conocen algunas tentativas de aplicar la solución analítica para la corrección del efecto de la atenuación (Hitschfeld and Bordan, 1954) o la aplicación de algunas metodologías simplificadas que evitan los problemas de la solución analítica.
Solución analítica
Si se acepta que la relación entre la atenuación específica (K) y la reflectividad efectiva (no atenuada, Ze) se puede expresar mediante una ley potencial (Atlas and Banks, 1951; Hitschfeld and Bordan, 1954):
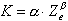
Ec. 4
la ecuación de la atenuación,
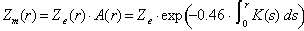
Ec. 5
se puede rescribir en función de la reflectividad medida (por un radar atenuado, Zm) como (Hitschfeld and Bordan, 1954):
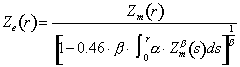
Ec. 6
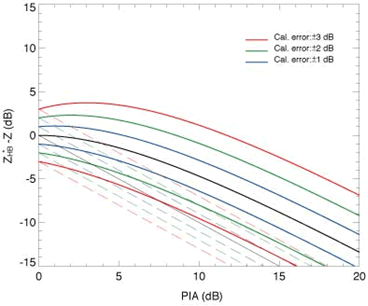
Como ya detectaron los mismos Hitschfeld y Bordan, esta ecuación tiene un comportamiento muy inestable cuando la medida del radar está afectada por pequeños errores (especialmente por pequeños errores en la calibración del radar) o los parámetros ? y ? no están perfectamente ajustados (ver Fig. 4 y Fig. 5).
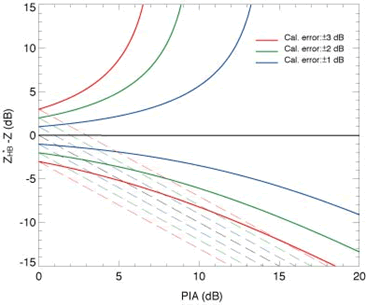
De esta forma, los mismos Hitschfeld y Bordan (1954) llegaron a la conclusión que la atenuación es un obstáculo insalvable para utilizar los radares de banda X para la medida cuantitativa de precipitación a menos que el error de calibración del radar se pudiese mantener en “límites extraordinariamente pequeños”. Históricamente, este artículo, supuso un punto de inflexión que provocó el progresivo abandono de las longitudes de onda más pequeñas (más atenuadas).
La necesidad de una corrección para los radares con frecuencias atenuadas (terrestres de banda C y sobre todo los radares situados en satélites) hicieron que a partir de los años 1980, se empezaran a desarrollar nuevos algoritmos de corrección. Algunos de ellos se describen a continuación.
Técnicas de corrección de la atenuación de la señal del radar debida a la precipitación
Las diferentes técnicas de corrección de la atenuación se pueden agrupar en la siguiente clasificación:
- Técnicas que evitan la no-convergencia de la ecuación de Hitschfeld y Bordan.
- Técnicas de Referencia de Superficie (Surface Reference Techniques).
- Técnicas dual-radar.
- Técnicas basadas en radares de doble longitud de onda.
- Técnicas basadas en radares con polarización múltiple.
En general, todas ellas (a excepción de las del primer grupo), se basan en utilizar diferentes ligaduras para evitar los problemas de inestabilidad que tiene la solución analítica (Ec. 6). A continuación, pasamos a explicar algunas de las técnicas de los tres primeros grupos, aplicables a los radares operativos más comunes.
Técnicas que evitan la no-convergencia de la ecuación de Hitschfeld y Bordan
La técnica más sencilla para evitar la inestabilidad de la ecuación de Hitschfeld y Bordan es la propuesta por Delrieu et al. (1997). Consiste en aplicar dicha ecuación, pero limitando la corrección a un máximo preestablecido (ellos proponen una corrección máxima de 10 dB; ver Fig. 6). De esta forma, si supusiéramos que no hay errores ni en la medida radar ni en la relación Z-K en las zonas de atenuación intensa se estaría subestimando la reflectividad real (no atenuada).
Otra técnica sencilla que evita la divergencia de la ecuación de Hitschfeld y Boradan consiste en corregir la señal mediante la Ec. 5, pero estimando la reflectividad real (no atenuada, Ze) mediante la reflectividad medida (atenuada, Zm) a la hora calcular el coeficiente de atenuación específica (K) con la Ec. 4:
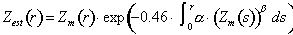
Ec. 7
De esta forma, en el caso de tener un radar perfectamente calibrado se estará subestimando la corrección por atenuación, pero se evitarán los problemas de inestabilidad de la Ec. 6 si hay errores en la medida del radar. Los errores que se cometerían corrigiendo de esta forma se pueden apreciar en la Fig. 7.
A partir de esta idea, Hildebrand (1978) y Meneghini (1978) por separado, propusieron un método iterativo para hacer la corrección por atenuación. Este método consiste en utilizar la reflectividad calculada en el paso anterior para estimar el coeficiente de atenuación específica (utilizando, para la primera iteración, la reflectividad medida por el radar):
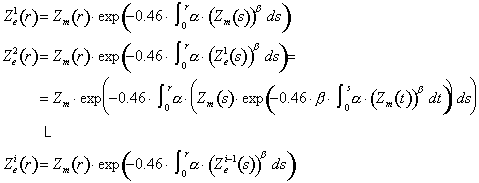
Ec. 8
Sin embargo, este método, tiende a la solución de Hitschfeld y Bordan (Meneghini, 1978), de modo que tiene los mismos problemas de inestabilidad con pequeños errores de la medida si se intenta hacer converger. Por esto, (Meneghini, 1978), propuso utilizar tan solo las dos primeras iteraciones.
En general, el problema que tienen estas metodologías es que es difícil cuantificar el error que se comete al aplicarlas.
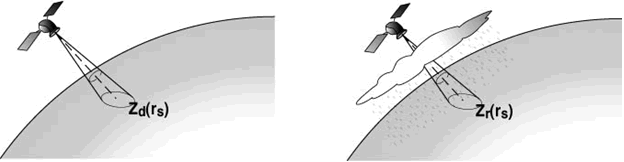
Técnicas de Referencia de Superficie (Surface Referente Techniques)
Este grupo de técnicas se desarrollaron cuando se empezaron a diseñar las misiones de radares transportados por satélites (Iguchi y Meneghini, 1994; Marzoug y Amayenc, 1994; Meneghini et al., 1983). Aunque existen diferentes formulaciones, consisten en hacer una estimación de la atenuación acumulada a lo largo del haz del radar desde el satélite hasta la superficie de la Tierra A(rs)=Zd(rs)-Zr(rs) (ver Fig. 8). Esta estimación se introduce en la ecuación de Hitschfeld y Bordan (Ec. 6) a modo de ligadura, con lo que se obtiene una nueva ecuación mucho más estable para corregir la atenuación a lo largo del haz.
A partir de la misma idea, el Método de la Referencia Orografía (Delrieu et al., 1997) propuso utilizar el retorno debido a la intercepción del haz con el terreno (ecos de suelo) para radares terrestres, estimando la atenuación a partir del retorno de las montañas en condiciones de aire claro y cuando el haz es interceptado por precipitación (ver Fig. 9).
Si bien esta metodología parece dar buenos resultados y evita completamente los problemas de estabilidad (Delrieu et al., 1997; Delrieu et al., 1999), su aplicación a radares terrestres presenta tres inconvenientes:
- Sólo permite la corrección en aquellas direcciones en que se encuentran ecos de suelo significativos (no es útil para corregir sobre el mar).
- La corrección más allá del eco de referencia tiene los mismos problemas que la ecuación de Hitschfeld y Bordan.
- Si está lloviendo sobre el eco de referencia, la corrección tiene dificultades muy importantes.
Técnicas dual-radar
Estas técnicas, desarrolladas tanto para radares montados en satélites (Testud y Amayenc, 1989) como para radares terrestres (Srivastava y Tian, 1996; Testud y Amayenc, 1989; Tian y Srivastava, 1997), consisten en utilizar las medidas de dos radares en la zona de intersección para imponer que en cada punto de esta región, los valores de reflectividad de ambos radares una vez corregidos tienen que coincidir. De esta forma, obtienen el coeficiente de atenuación específica, con el que se puede obtener la reflectividad no atenuada.
Estos métodos tienen algunas ventajas que los hacen atractivos, como pueden ser la insensibilidad a los errores de calibración del radar y el hecho de que no necesitan formular ninguna hipótesis sobre la relación entre la reflectividad (Ze) y el coeficiente de atenuación específica (K). Así y todo, estos métodos presentan algunos inconvenientes para su aplicación operativa como pueden ser las dificultades geométricas, o el hecho de que sólo se pueden aplicar en el volumen de intersección de los escaneos de los dos radares.
La relación Z-K
A parte de lo expuesto hasta este punto, otra dificultad de la corrección de la atenuación estriba en la determinación de los parámetros ? y ? de la relación Z-K (Ec. 4). Estos coeficientes dependen fundamentalmente de los siguientes factores (ver, por ejemplo Battan, 1973; Delrieu et al., 1991; Doviak y Zrnic, 1992):
Longitud de onda del radar: una misma precipitación atenúa mucho más la señal de los radares de longitudes de onda más cortas (banda X o K) que la de un radar de banda S (en qué a?0); (Burrows y Attwood, 1949) proponen para T=0ºC en situación de tormenta, a=5,6?10-5 y b=0,86 para el caso de un radar de banda X, y a=5,4?10-6 y b=0,69 para otro de banda S). (Delrieu et al., 1991) proponen a=6,74?10-5 y b=0,80 para un radar de banda X y a=1,22?10-5 y b=0,84para radares de banda C.
La temperatura influye en la sección transversal de la atenuación.
Clase y fase de precipitación: al variar la DSD (Drop Size Distribution), los parámetros de la relación Z-K (como los de la relación Z-R) también cambian (ver (Sempere-Torres et al., 1994)).
Como conclusión final, queremos mencionar que el efecto de la atenuación de la señal de los radares meteorológicos con longitudes de onda inferiores a 10 cm es significativo (dramático para radares de banda X e inferiores). La mayoría de estudios que se han hecho respecto a este fenómeno inciden en la gran dificultad de corregir los radares de banda X y en la necesidad de aplicar algún tipo de corrección para los radares de banda C si se quieren utilizar para desde un punto de vista cuantitativo (Delrieu et al., 2000; Duncan et al., 1991). A pesar de ello, en muy pocos radares operativos (mayoritariamente de banda C a excepción de Estados Unidos –banda S-) se aplica algún tipo de corrección debido a la incertidumbre sobre la bondad de las correcciones más sencillas.
CONCLUSIONES
La utilización del radar meteorológico con fines hidrológicos está altamente condicionada por un grupo de fenómenos asociados intrínsecamente al modo de funcionamiento de la herramienta y a las características atmosféricas y todo ello implica que la fiabilidad cuantitativa de las medidas sea todavía bastante baja. La interpretación cualitativa de estas imágenes, tanto en las tareas de diagnóstico y predicción inmediata, como en el análisis del campo de precipitación acumulada, también está limitada por algunos efectos como el de la atenuación del haz en su camino de ida y vuelta al radar o el apantallamiento orográfico.
La atenuación por gases y especialmente por hidrometeoros es importante especialmente para radares de longitud de onda relativamente corta (bandas X y C) y es mucho menos significativa en radares de banda S, de coste económico, sin embargo, muy superior. Es muy notable la pérdida de potencia que se produce en el haz cuando éste atraviesa un área extensa de precipitación estratiforme de intensidad moderada u otra más reducida de precipitación convectiva fuerte o muy fuerte.
A pesar del importante efecto de la atenuación de la señal debida a la precipitación sobre la medida de los radares con longitudes de onda por debajo de los 10 cm, no es habitual que los radares meteorológicos operativos tengan implementada ninguna técnica de corrección de este fenómeno (recientemente, se han empezado a incluir algunas técnicas muy simples –basadas en la Ec. 7- en algunos paquetes de software para tratamiento de las medidas radar).
La razón por la no implementación de algoritmos de corrección es su dificultad, debida principalmente a la inestabilidad de la solución analítica (Ec. 6) ante pequeños errores de la medida radar y en la estimación de los parámetros de la relación Z-K. Ante esta inestabilidad, las nuevas metodologías de corrección se basan en imponer ligaduras a la ecuación de Hitschfeld y Bordan (1954), lo que permiten convertirla en una ecuación mucho más estable. A pesar de ello, estas nuevas técnicas no se implementan operativamente debido a las distintas dificultades y limitaciones comentadas en el texto.
REFERENCIAS
Atlas, D. y Banks, H.C., 1951. The interpretation of microwave reflections from rainfall. J. Meteor., 8(5): 271-282.
Atlas, D. (Ed.), 1990. Radar in Meteorology. American Meteorological Society, Boston.
Battan, L.J., 1973. Radar Observation of the Atmosphere. University of Chicago Press, Chicago (USA), 324 pp.
Burrows, D.R. y Attwood, S.S., 1949. Radio Wave Propagation, New York, USA, 219 pp.
Delrieu, G., Andrieu, H. y Creutin, J.D., 2000. Quantification of path-integrated attenuation for X- and C-Band weather radar systems operating in Mediterranean heavy rainfall. J. Appl . Meteor., 39: 840-850.
Delrieu, G., Caoudal, S. y Creutin, J.D., 1997. Feasibility of using mountain return for the correction of ground-based X-band weather radar data. J. Atmos. Oceanic Technol., 14: 368-385.
Delrieu, G., Creutin, J.D. y Saint-André, I., 1991. Mean K-R relationships: Practical results for typical radar wavelengths. J. Atmos. Oceanic Technol., 8(4): 467-476.
Delrieu, G., Serrar, S., Guardo, E. y Creutin, J.-D., 1999. Rain measurement in hilly terrain with X-Band weather radar systems: accuracy path-integrated attenuation estimates derived from mountain returns. J. Atmos. Oceanic Technol., 16: 405-416.
Doviak, R.J. y Zrnic, D.S., 1992. Doppler radar and weather observations. Academic Press, San Diego, CA (USA), 562 pp.
Duncan, M.R., Bellon, A., Austin, G.L. y Cluckie, I., 1991. Attenuation effects in C and X-band radar used for urban hydrology, 25th Conf. on Radar Meteor. AMS, Paris, France.
Hildebrand, P.H., 1978. Iterative correction for attenuation of 5 cm radar in rain. J. Appl . Meteor., 17: 508-514.
Hitschfeld, W.F. y Bordan, J., 1954. Errors inherent in the radar measurement of rainfall at attenuating wavelengths. J. Meteor., 11: 58-67.
Iguchi, T. y Meneghini, R., 1994. Intercomparison of single-frequency methods for retrieving a vertical rain profile from airborne or spaceborne radar data. J. Atmos. Ocean. Tech., 11: 1507-1516.
Marzoug, M. y Amayenc, P., 1994. A class of single- and dual-frequency algorithms for rain-rate profiling form a spaceborne radar. Part I: Principle and tests from numerical simulations. J. Atmos. Oceanic Technol., 11: 1480-1506.
Meneghini, R., 1978. Rain-rate estimates for an attenuating radar. Radio Sci., 13(3): 459-470.
Meneghini, R., Eckerman, J. y Atlas, D., 1983. Determination of rain rate from a spaceborne radar using measurements of total attenuation. IEEE Trans. Geosci. Remote Sensing, 21: 34-43.
Rinehart, R., 1997. Radar for Meteorologists. Rinehart Publications, Grand Forks.
Sempere-Torres, D., Porrà, J.M. y Creutin, J.D., 1994. A general formulation for rain drop size distribution. J. Appl. Meteor., 33(12): 1494-1502.
Srivastava, R.C. y Tian, L., 1996. Measurement of Attenuation by a dual-radar method. Concept and error analysis. J. Atmos. Oceanic Technol., 13: 937-947.
Testud, J. y Amayenc, P., 1989. Stereoradar meteorology: a promising technique for observation of precipitation from a mobile platform. J. Atmos. Oceanic Technol., 6: 89-108.
Tian, L. y Srivastava, R.C., 1997. Measurement of attenuation at C band in a convective storm by a dual-radar method. J. Atmos. Oceanic Technol., 14: 184-196.
Y también documentación interna elaborada por el Servicio de Teledetección del I.N.M.